Subjek:Matematika/Materi:Diferensial

Turunan atau Derivatif dalam ilmu kalkulus merupakan pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai masukan. Secara umum, turunan menyatakan bagaimana suatu fungsi berubah akibat perubahan variabel; contohnya, turunan dari posisi sebuah benda bergerak terhadap waktu adalah kecepatan sesaat objek tersebut.

Definisi

$f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}$

Biaya marjinal

$\lim _{h\to 0}{\frac {\Delta C}{h}}=\lim _{h\to 0}{\frac {C(x+h)}{h}}=C'(x)$

Sifat turunan

Dalam hal ini, Templat:Math, untuk bilangan riil Templat:Math dan Templat:Math dan kemiringan Templat:Math diberikan oleh

$m={\frac {{\text{mengalih pada }}y}{{\text{mengalih pada }}x}}={\frac {\Delta y}{\Delta x}},$

Apa itu simbol Templat:Math adalah singkatan untuk perubahan. $\Delta y=f(x+\Delta x)-f(x)$

Rumus di atas berlaku karena

${\begin{aligned}y+\Delta y&=f\left(x+\Delta x\right)\\&=m\left(x+\Delta x\right)+b=mx+m\Delta x+b\\&=y+m\Delta x.\end{aligned}}$

Hasilnya adalah

$\Delta y=m\Delta x.$

Nilai tersebut memberikan untuk kemiringan garis.

Nilai perubahan sebagai nilai limit

Gambar 1. Garis singgung pada (x, f(x))

Gambar 2. The secant to curve y= f(x) determined by points (x, f(x)) and (x + h, f(x + h))

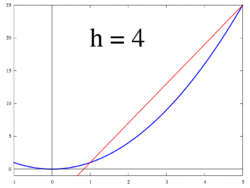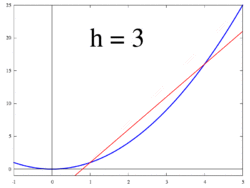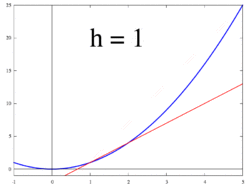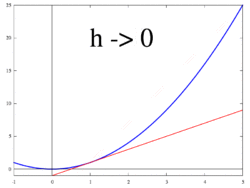
Gambar 3. Garis singgung sebagai batas garis potong

Gambar 4. Ilustrasi animasi: garis singgung (turunan) sebagai batas garis potong

Sifat - sifat turunan

Linearitas

• ${\frac {d}{dx}}(u\pm v)=u'\pm v'\,$
• ${\frac {d}{dx}}(nu)=n{\frac {du}{dx}}\,$

Aturan produk

• ${\frac {d}{dx}}(uv)=u'v+uv'\,$

Dalil rantai

• ${\frac {dy}{dx}}={\frac {dy}{dv}}\cdot {\frac {dv}{du}}\cdot {\frac {du}{dx}}\,$

Sifat umum lain

• ${\frac {d}{dx}}({\frac {u}{v}})={\frac {u'v-uv'}{v^{2}}}\,$
• ${\frac {d}{dx}}(x^{n})=nx^{n-1}\,$
• ${\frac {d}{dx}}(u^{n})=nu^{n-1}\cdot {\frac {du}{dx}}$

Dimana fungsi $u$ dan $v$ adalah fungsi satu variabel $x$.

Eksponen dan bilangan natural

• ${\frac {d}{dx}}(e^{x})=e^{x}\,$
• ${\frac {d}{dx}}(a^{x})=a^{x}\ln {a}\,$

Logaritma dan bilangan natural

• ${\frac {d}{dx}}(\ln {x})={\frac {1}{x}}\,$
• ${\frac {d}{dx}}(\log _{a}{x})={\frac {1}{x\ln {a}}}\,$

Trigonometri

• ${\frac {d}{dx}}(\sin {x})=\cos {x}\,$
• ${\frac {d}{dx}}(\cos {x})=-\sin {x}\,$
• ${\frac {d}{dx}}(\tan {x})=\sec ^{2}{x}\,$
• ${\frac {d}{dx}}(\cot {x})=-\csc ^{2}{x}\,$
• ${\frac {d}{dx}}(\sec {x})=\sec {x}\tan {x}\,$
• ${\frac {d}{dx}}(\csc {x})=-\csc {x}\cot {x}\,$

Invers

• ${\frac {d}{dx}}(\arcsin x)={\frac {1}{\sqrt {1-x^{2}}}}$
• ${\frac {d}{dx}}(\arccos x)={\frac {-1}{\sqrt {1-x^{2}}}}$
• ${\frac {d}{dx}}(\arctan x)={\frac {1}{1+x^{2}}}$
• ${\frac {d}{dx}}(\operatorname {arccot} x)={\frac {-1}{1+x^{2}}}$
• ${\frac {d}{dx}}(\operatorname {arcsec} x)={\frac {1}{x{\sqrt {x^{2}-1}}}}$
• ${\frac {d}{dx}}(\operatorname {arccsc} x)={\frac {-1}{x{\sqrt {x^{2}-1}}}}$

Hiperbolik

• ${\frac {d}{dx}}(\sinh {x})=\cosh {x}\,$
• ${\frac {d}{dx}}(\cosh {x})=\sinh {x}\,$
• ${\frac {d}{dx}}(\tanh {x})={\text{sech}}^{2}\,{x}\,$
• ${\frac {d}{dx}}(\coth {x})=-{\text{csch}}^{2}{x}\,$
• ${\frac {d}{dx}}({\text{sech}}\,{x})=-{\text{sech}}\,{x}\tanh {x}$
• ${\frac {d}{dx}}({\text{csch}}\,{x})=-{\text{csch}}\,{x}\coth {x}$

Contoh soal dalam aplikasi turunan

NB

hasil nilai turunan pada maksimum/terbesar atau minimum/terkecil dianggap nol agar tercapai.

• Tentukan persamaan garis yang menyinggung kurva $y=x^{3}+2x^{2}-5x$ di titik $(1,-2)$!

$y=x^{3}+2x^{2}-5x$

$m=y'=3x^{2}+4x-5$

masukkan x = 1 untuk menentukan nilai m

$m=y'=3(1)^{2}+4(1)-5=2$

persamaan garis singgung dengan gradien 2 dan melalui titik (1,-2)

$y-y_{1}=m(x-x_{1})$

$y-(-2)=2(x-1)$

$y=2x-4$

• Tentukan persamaan garis yang tegak lurus dengan kurva $y=x^{3}+2x^{2}-5x$ di titik $(1,-2)$!

$y=x^{3}+2x^{2}-5x$

$m=y'=3x^{2}+4x-5$

masukkan x = 1 untuk menentukan nilai m

$m=y'=3(1)^{2}+4(1)-5=2$

karena tegak lurus maka nilai m_t

$m_{t}=-{\frac {1}{m}}$

$m_{t}=-{\frac {1}{2}}$

persamaan garis singgung dengan gradien 2 dan melalui titik (1,-2)

$y-y_{1}=m_{t}(x-x_{1})$

$y-(-2)=-{\frac {1}{2}}(x-1)$

$2(y+2)=-x+1$

$2y+4=-x+1$

$2y=-x-3$

• Suatu proyek pembangunan gedung sekolah dapat diselesaikan dalam x hari dengan biaya proyek per hari $3x-900+{\frac {120}{x}}$ ratus ribu rupiah. Berapa hari agar biaya minimum maka proyek tersebut diselesaikan?

biaya dalam 1 hari $B(1)=3x-900+{\frac {120}{x}}$

biaya dalam x hari $B(x)=x(3x-900+{\frac {120}{x}})$

$B(x)=3x^{2}-900x+120$

biaya minimum tercapai saat turunannya = 0

$B'(x)=0$

$B'(x)=6x-900=0$

$6x=900$

$x=150$ hari

• Suatu perusahaan menghasilkan x produk dengan biaya total sebesar $75+2x+0,1x^{2}$ ribu rupiah. Jika semua produk perusahaan terjual dengan harga Rp40,000 untuk setiap produknya. Berapa laba maksimum yang diperolehnya?

laba = total penjualan - total biaya

laba $L(x)=40x-(75+2x+0,1x^{2})$

$L(x)=-75+38x-0,1x^{2}$

laba maksimum tercapai saat turunannya = 0

$L'(x)=0$

$L'(x)=38-0,2x=0$

$0,2x=38$

$x=190$

$L(190)=-75+38(190)-0,1(190)^{2}$

$L(190)=-75+7,220-3,610$

$L(190)=3,535$ ribu rupiah

• Jumlah dari bilangan pertama dan bilangan kedua kuadrat adalah 75. Berapa nilai terbesar dari hasil kali?

Misalkan: bilangan pertama = x dan bilangan kedua = y

$x+y^{2}=75$

$x=75-y^{2}$

hasil kali: $f(y)=x\cdot y$

$f(y)=(75-y^{2})\cdot y$

$f(y)=75y-y^{3}$

nilai terbesar dari hasil kali tercapai saat turunannya = 0

$f'(y)=0$

$f'(y)=75-3y^{2}=0$

$3y^{2}=75$

$y^{2}=25$

$y_{1}=5atauy_{2}=-5$

karena nilai terbesar maka terambil y = 5, kita cari x

$x=75-(5)^{2}$

$x=50$

nilai terbesar hasil kali: $50\cdot 5=250$